Intercept Adjustment • predtools


library(predtools)
library(magrittr)
library(dplyr)
#> 
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union
library(ggplot2)

What is intercept adjustment?

In clinical prediction modeling, model updating refers to the practice of modifying a prediction model before it is used in a new setting to improve its performance. One of the simplest updating methods for risk predication models is a fixed odds-ratio transformation of predicted risks to improve the model’s calibration-in-the-large.

interceptAdj function uses an approximate equation for recovering the conditional odds-ratio from the observed mean and predicted variance of risks in validation and development sets, respectively.

A step-by-step guide.

Imagine the variable y indicates risk of disease recurrence in a unit of time. We have a prediction model that quantifies this risk given a patient’s age, disease severity level, sex, and whether the patient has a comorbidity.

The package comes with two exemplary datasets. dev_data and val_data. We use the dev_data as the development sample and the val_data as the external validation sample.

Model updating matters when there is a considerable difference between mean of the observed risks in development and validation sets. The average of y in the above two datasets are almost identical. Therefore, to have a meaningful scenario, we create a secondary (arbitrary) outcome (y_alt) in val_data with a lower average (by ~ 50%).


data(dev_data)
data(val_data)

	y	y_alt
	Min. :0.0000	Min. :0.00
	1st Qu.:0.0000	1st Qu.:0.00
	Median :0.0000	Median :0.00
	Mean :0.2975	Mean :0.12
	3rd Qu.:1.0000	3rd Qu.:0.00
	Max. :1.0000	Max. :1.00

dev_data has 500 rows. val_data has 400 rows.

Here are the first few rows of dev_data:

age	severity	sex	comorbidity	y
55	0	0	1	1
52	1	0	0	0
63	0	0	1	0
61	1	1	1	1
58	0	1	0	0
54	1	0	0	1
45	0	0	0	0

We use the development data to fit a logistic regression model as our risk prediction model:


reg<-glm(y~sex+age+severity+comorbidity,data=dev_data,family=binomial(link="logit"))
summary(reg)
#> 
#> Call:
#> glm(formula = y ~ sex + age + severity + comorbidity, family = binomial(link = "logit"), 
#>     data = dev_data)
#> 
#> Coefficients:
#>              Estimate Std. Error z value Pr(>|z|)    
#> (Intercept) -1.728929   0.565066  -3.060  0.00222 ** 
#> sex          0.557178   0.223631   2.492  0.01272 *  
#> age          0.005175   0.010654   0.486  0.62717    
#> severity    -0.557335   0.227587  -2.449  0.01433 *  
#> comorbidity  1.091936   0.209944   5.201 1.98e-07 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 602.15  on 499  degrees of freedom
#> Residual deviance: 560.41  on 495  degrees of freedom
#> AIC: 570.41
#> 
#> Number of Fisher Scoring iterations: 4

Given this, our risk prediction model can be written as:

\(\bf{ logit(p)=-1.7289+0.5572*sex+0.0052*age-0.5573*severity+1.0919*comorbidity}\).

First, let’s see the calibration plot in development and validation datasets. We use calibration_plot from our package to create calibration plots.


dev_data$pred <- predict.glm(reg, type = 'response')
val_data$pred <- predict.glm(reg, newdata = val_data, type = 'response')

calibration_plot(data = dev_data, obs = "y", pred = "pred", title = "Calibration plot for development data")
#> $calibration_plot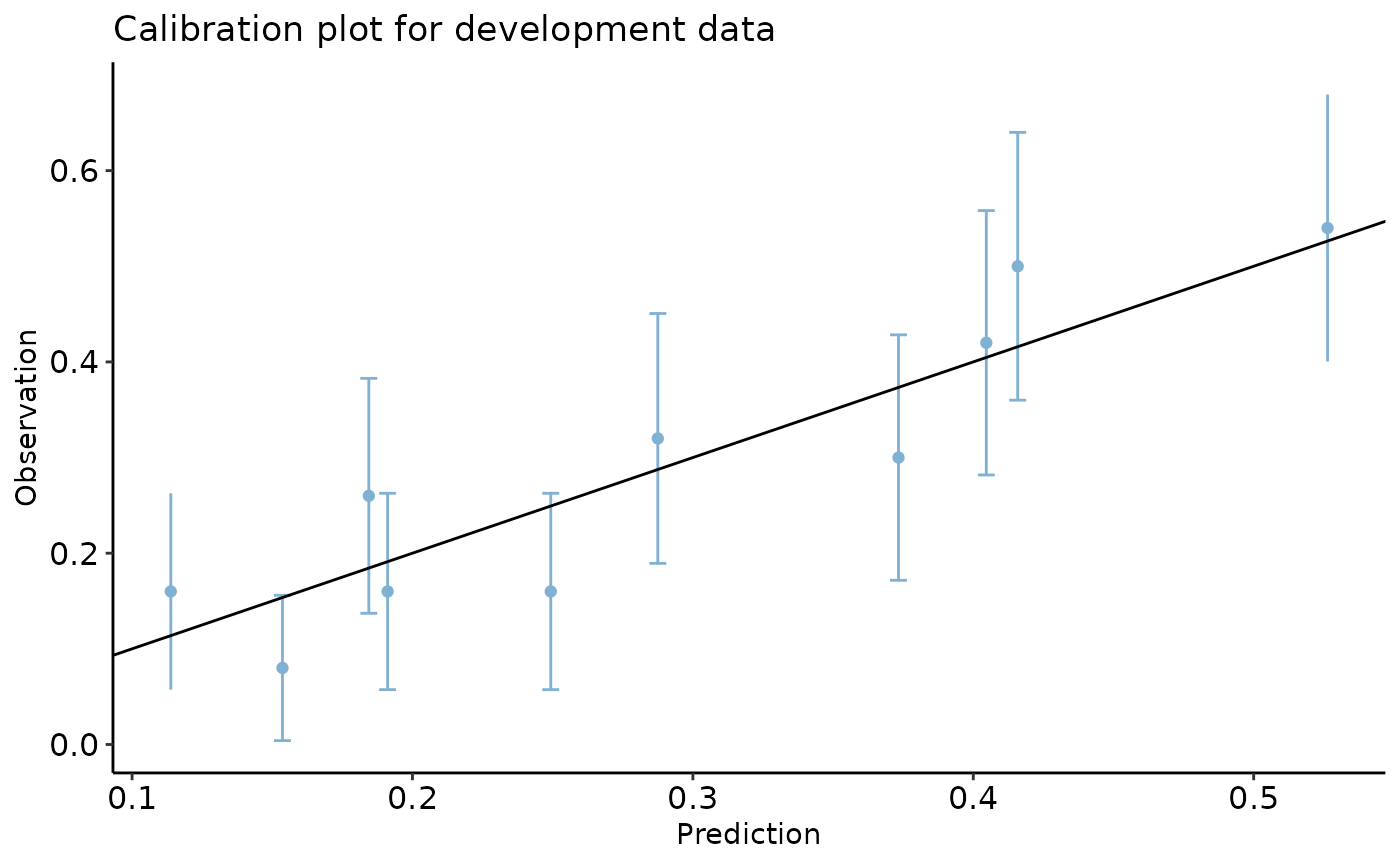

calibration_plot(data = val_data, obs = "y_alt", pred = "pred", y_lim = c(0, 0.6),
                 title = "Calibration plot for validation data")
#> $calibration_plot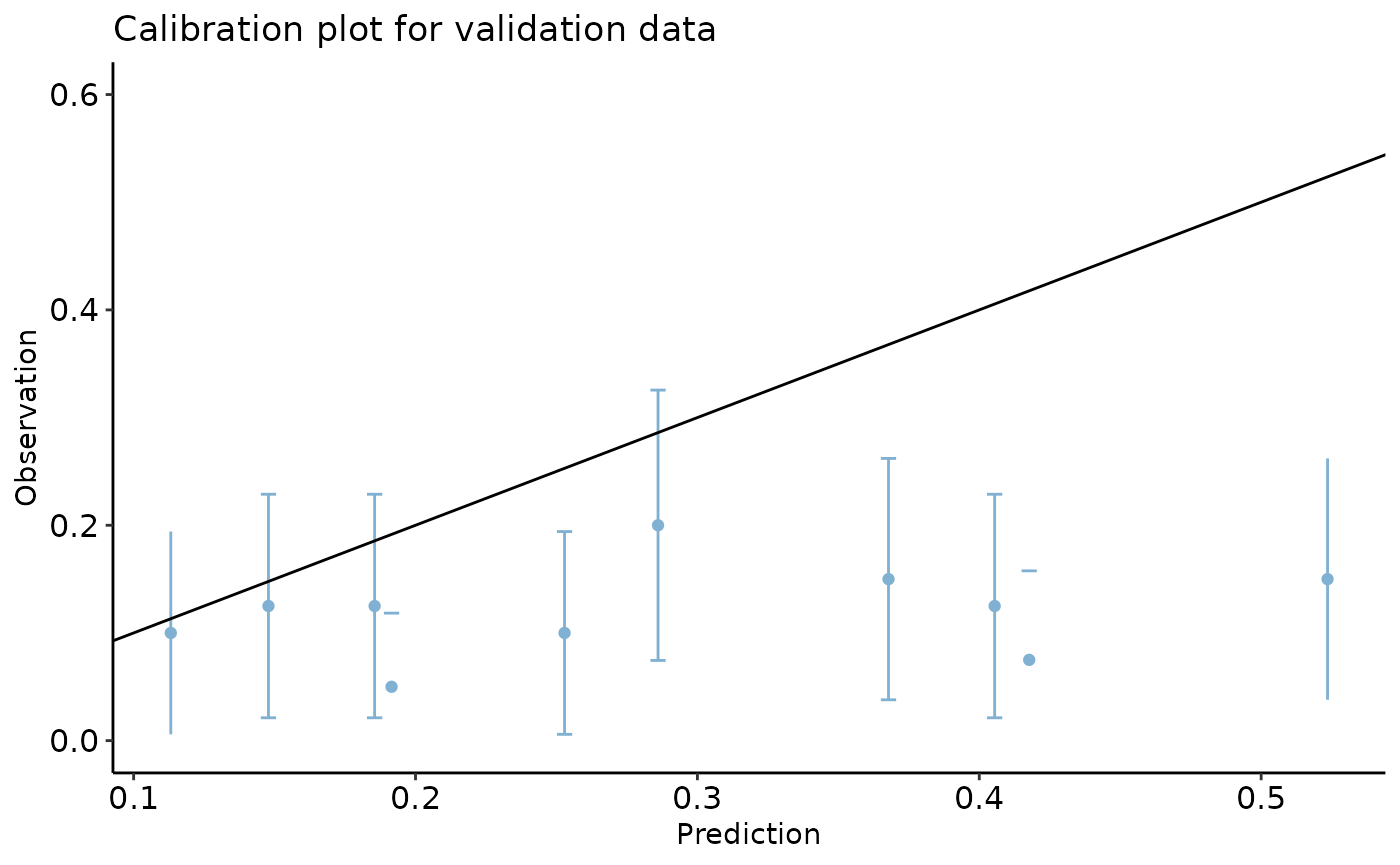

To adjust the predicted risks for the validation set, we estimate the correction factor by using function odds_adjust:


odds_correction_factor <- odds_adjust(p0 = mean(dev_data$y), p1 = mean(val_data$y_alt), v = var(dev_data$pred))
odds_correction_factor
#> [1] 0.3116119

We can now recalibrate the predictions and reproduce the calibration plot for the validation set.


dev_data$pred <- predict.glm(reg, type = 'response')
val_data$pred <- predict.glm(reg, newdata = val_data, type = 'response')

val_data$odds_adj <- (val_data$pred / (1 - val_data$pred)) * odds_correction_factor
val_data$pred_adj <- val_data$odds_adj / (1 + val_data$odds_adj)

val_data$id <- c(1 : nrow(val_data))
val_data_long <- reshape(data = val_data, direction = "long", varying = c("pred", "pred_adj"), v.name = "preds",
                         idvar = "id", timevar = "Method", times = c("Primitive", "Adjusted"))

calibration_plot(data = val_data, obs = "y_alt", pred = "pred_adj",
                 title = "Calibration plot for development data - after recalibration")
#> $calibration_plot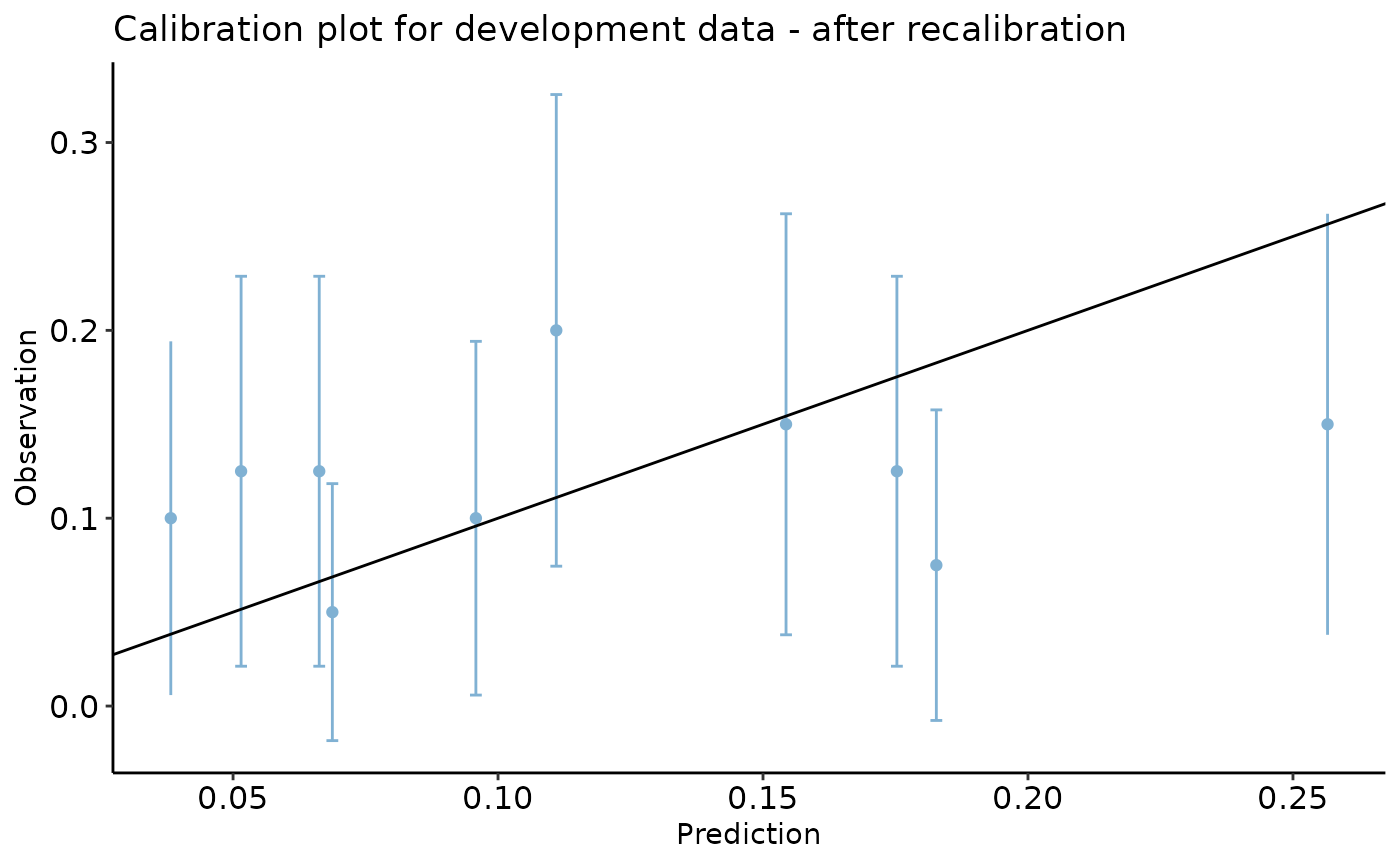

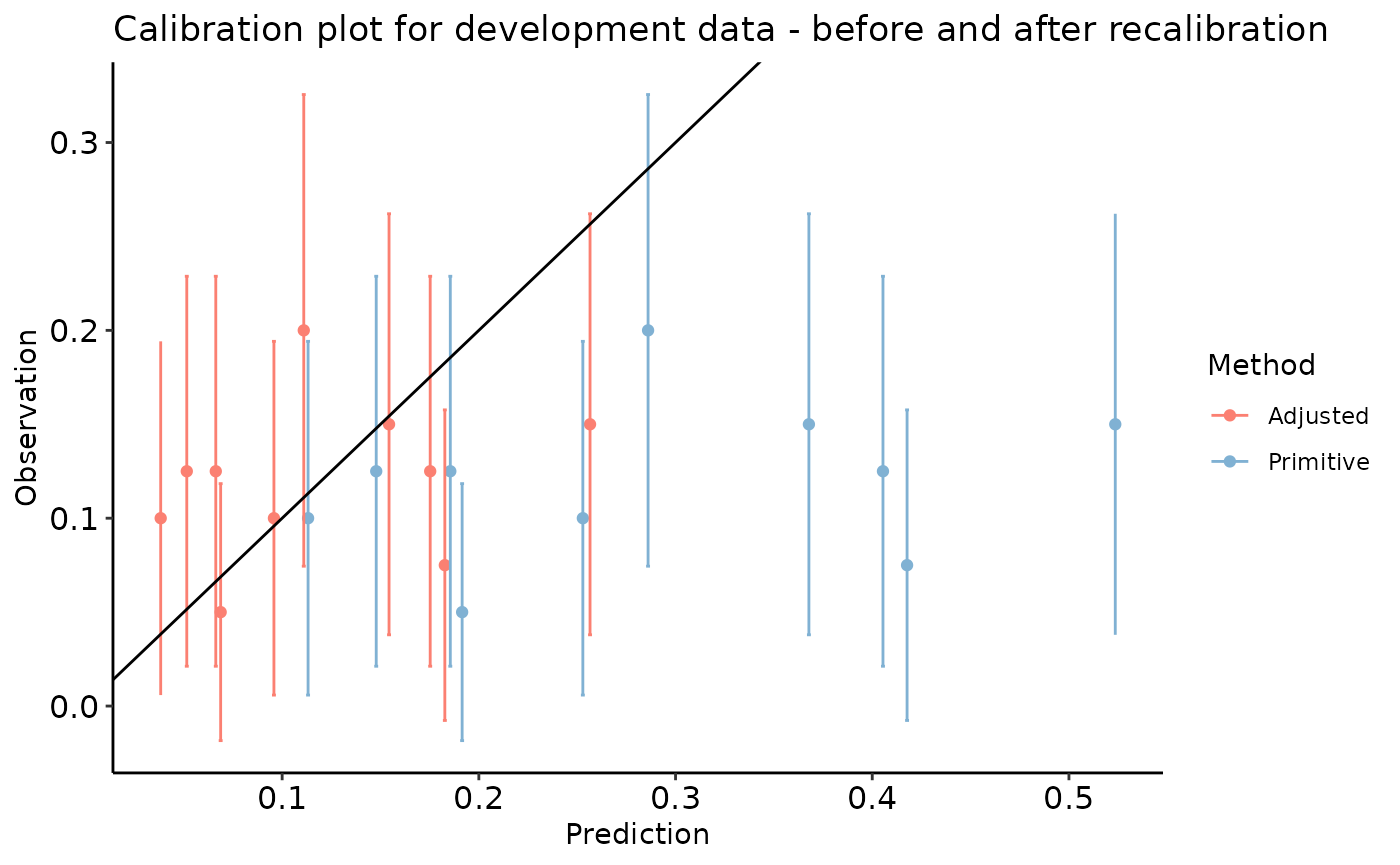
calibration_plot(data = val_data_long, obs = "y_alt", pred = "preds", group = "Method",
                 title = "Calibration plot for development data - before and after recalibration")
#> $calibration_plot